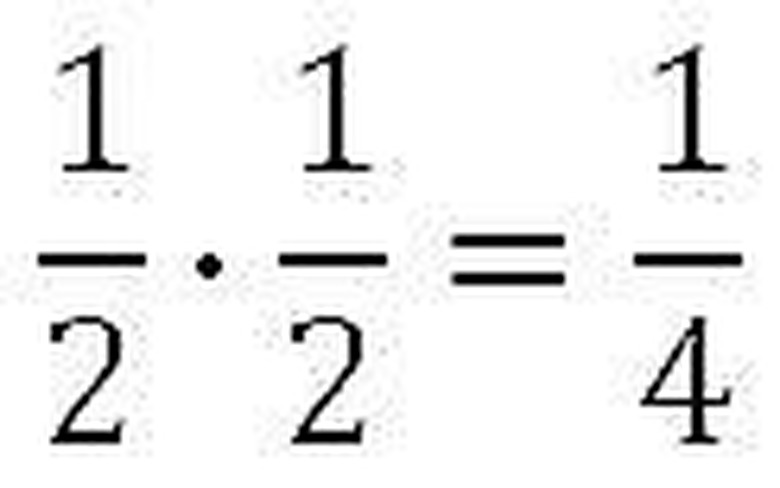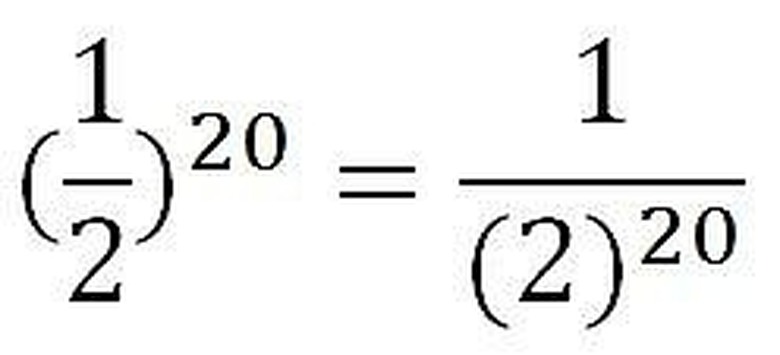How To Solve Basic Probability Problems Involving A Coin Flip
This is Article 1 in a series of stand-alone articles on basic probability. A common topic in introductory probability is solving problems involving coin flips. This article shows you the steps for solving the most common types of basic questions on this subject.
Step 1
First, note that the problem will likely make reference to a "fair" coin. All this means is that we're not dealing with a "trick" coin, such as one which has been weighted to land on a certain side more often than it would have.
Step 2
Second, problems such as this never involve any type of silliness, such as the coin landing on its edge. Sometimes students try to lobby to have a question deemed null-and-void because of some far-fetched scenario. Don't bring anything into the equation such as wind-resistance, or whether Lincoln's head weighs more than his tail, or any such thing. We're dealing with 50/50 here. Teachers really get upset with talk of anything else.
Step 3
With all that said, here is a very common question: "A fair coin lands on heads five times in a row. What are the chances that it will land on heads on the next flip?" The answer to the question is simply 1/2 or 50% or 0.5. That is it. Any other answer is wrong.
Step 4
Stop thinking about whatever it is that you are thinking about right now. Each flip of a coin is totally independent. The coin does not have a memory. The coin does not get "bored" of a given outcome, and desire to switch to something else, nor does it have any desire to continue a particular outcome since it's "on a roll." To be sure, the more times you flip a coin, the closer you will get to 50% of the flips being heads, but that still has nothing to do with any individual flip. These ideas comprise what is known as the Gambler's Fallacy. See the Resource section for more.
Step 5
Here is another common question: "A fair coin is flipped twice. What are the chances that it will land on heads on both flips?" What we are dealing with here is two independent events, with an "and" condition. Stated more simply, each flip of the coin has nothing to do with any other flip. Additionally, we are dealing with a situation where we need one thing to occur, "and" another thing.
Step 6
In situations such as the above, we multiply the two independent probabilities together. In this context, the word "and" translates to multiplication. Each flip has a 1/2 chance of landing on heads, so we multiply 1/2 times 1/2 to get 1/4. That means that each time we conduct this two-flip experiment, we have a 1/4 chance of getting heads-heads as the outcome. Note that we could have also done this problem with decimals, to get 0.5 times 0.5 = 0.25.
Step 7
Here is the final model of question discussed in this article: "A fair coin is flipped 20 times in a row. What are the chances that it will land on heads every time? Express your answer using an exponent." As we saw before, we are dealing with an "and" condition for independent events. We need the first flip to be heads, and the second flip to be heads, and the third one, etc.
Step 8
We must compute 1/2 times 1/2 times 1/2, repeated a total of 20 times. The simplest way of representing this is shown at left. It is (1/2) raised to the 20th power. The exponent is applied to both the numerator and the denominator. Since 1 to the power of 20 is just 1, we could also just write our answer as 1 divided by (2 to the 20th power).
Step 9
It is interesting to note that the actual odds of the above happening are about one in a million. While it is unlikely that any one particular person will experience this, if you were to ask every single American to conduct this experiment honestly and accurately, quite a number of people would report success.
Step 10
Students should make sure that they are comfortable working with the basic probability concepts discussed in this article since they come up quite frequently.
Cite This Article
MLA
Contributor, . "How To Solve Basic Probability Problems Involving A Coin Flip" sciencing.com, https://www.sciencing.com/probability-problems-involving-coin-flip-4745644/. 24 April 2017.
APA
Contributor, . (2017, April 24). How To Solve Basic Probability Problems Involving A Coin Flip. sciencing.com. Retrieved from https://www.sciencing.com/probability-problems-involving-coin-flip-4745644/
Chicago
Contributor, . How To Solve Basic Probability Problems Involving A Coin Flip last modified March 24, 2022. https://www.sciencing.com/probability-problems-involving-coin-flip-4745644/